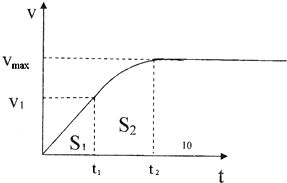
一列机车的质量是5×105kg,在水平平直轨道上由静止开始匀加速启动,加速度大小为0.4m/s2.已知机车的额定功率为3000kw,当机车由静止达到最大速率30m/s时,共用时t秒.行驶过程中阻力恒定,则:
(1)机车匀加速阶段的牵引力多大?
(2)匀加速阶段机车的实际功率等于额定功率时,机车的速度多大?
(3)机车由静止达到最大速度时,前进的距离是多少?(答案中可以包含字母t)
(1)当机车匀速运动时,速度达到最大值,此时牵引力等于阻力,F=f,此时P=Fv=fv,机车受到的阻力
f=
=P额 v最大
=1×105N,3×106W 30m/s
匀加速阶段,由牛顿第二定律可得:
F牵-f=ma,解得:F牵=3×105N;
(2)设匀加速阶段末的汽车速度为v1,
匀加速阶段机车的实际功率等于额定功率时,
由P=Fv,可得此时机车的速度v1=
=P额 F牵
=10m/s;3×106W 3×105N
(3)如图所示,达到最大速度前,有两个运动阶段.设匀加速阶段位移为s1,加速度减小阶段位移为s2.
匀加速阶段位移为:s1=
=v 21 2a
=125m,所用时间为t1=102 2×0.4
=v1 a
=25s,10 0.4
对于变加速阶段,由动能定理得:P(t-t1)-fs2=
mv最大2-1 2
mv12,1 2
解得:s2=(30t-2750)m,
所以,机车由静止到达最大速度时,前进的距离是:
s=s1+s2=(30t-2625)m;
答:(1)机车匀加速阶段的牵引力1×105N.
(2)匀加速阶段机车的实际功率等于额定功率时,机车的速度10m/s.
(3)机车由静止达到最大速度时,前进的距离是=(30t-2625)m.