问题
解答题
已知直线l的倾斜角为135°，且经过点P（1，1），
（Ⅰ）求直线l的方程；
（Ⅱ）求点A（3，4）关于直线l的对称点A′的坐标。
答案
解：（Ⅰ）∵k=tan135°=-1，
∴l：y-1=-（x-1），即x+y-2=0；
（Ⅱ）设A′（a， b），
则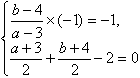
，
解得a=-2，b=-1，
∴A′（-2，-1）。
搜题请搜索小程序“爱下问搜题”
已知直线l的倾斜角为135°，且经过点P（1，1），
（Ⅰ）求直线l的方程；
（Ⅱ）求点A（3，4）关于直线l的对称点A′的坐标。
解：（Ⅰ）∵k=tan135°=-1，
∴l：y-1=-（x-1），即x+y-2=0；
（Ⅱ）设A′（a， b），
则，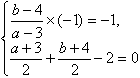
解得a=-2，b=-1，
∴A′（-2，-1）。
请在“考试项目”菜单上选择“电子表格软件使用”菜单项，完成下面的内容。
所有的电子表格文件都必须建立在指定的文件夹中。
1．打开工作簿文件EXl2.XLS(内容如下)，将工作表sheetl的Al:D1单元格合并为一个单元格，内容居中，计算“总计”行的内容，将工作表命名为“费用支出情况表”。
| A | B | C | D | |
| 1 | 公司费用指出情况 | |||
| 2 | 季度 | 工资 | 办公用品 | 房租 |
| 3 | 第一季度 | 25 | 15 | 50 |
| 4 | 第二季度 | 30 | 10 | 56 |
| 5 | 第三季度 | 35 | 8 | 55 |
| 6 | 总计 | |||