问题
问答题
设矩阵
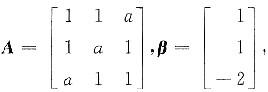已知线性方程组AX=β有解但不唯一，试求：
(1)α的值；(2)正交矩阵Q，使TAQ为对矩阵．
答案
参考答案：(1)对线性方程组AX=β的增广矩阵作行的初等变换，有
[*]
因为方程组AX=β有解但不唯一，所以秩r(A)=[*]＜3，故α=-2．
(2)[*]对应特征方程为
|λE-A|=λ(λ-3)(λ+3)．
得特征值为λ1=3，λ2=-3，λ3=0．
对应特征向量分别为α1=(1，0，-1)T，α2=(1，-2，1)T，α3=(1，1，1)T．
将α1，α2，α3单位化，得
[*]
令
[*]
则有
[*]tu/1012/yjs/s1218.390ECF.jpgtu/1012/yjs/s1218.397C00.jpgtu/1012/yjs/s1218.39FBEE.jpgtu/1012/yjs/s1218.3C5281.jpgtu/1012/yjs/s1218.3C9B03.jpgtu/1012/yjs/s1218.3CD0B9.jpg
解析：[考点提示] 矩阵的特征向量及特征值的计算问题．
