问题
解答题
已知平行四边形的两条边所在的直线方程分别是x+y+1=0和3x﹣y+4=0,它的对角线的交点是M(3,0),求这个四边形的其它两边所在的直线方程。
答案
解:由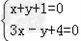 的相邻两条边的交点为
的相邻两条边的交点为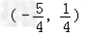 ,
,
又对角线的交点为M(3,0),
由中点坐标公式得:
另两条边的交点为(2×3﹣(﹣ ),2×0﹣
),2×0﹣ )即
)即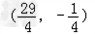 ,
,
且这两条边所在直线的斜率分别等于直线x+y+1=0和3x﹣y+4=0的斜率,为﹣1和3,
由点斜式知,所求两条直线的方程为y﹣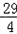 =﹣(x+
=﹣(x+ )和y﹣
)和y﹣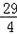 =3(x+
=3(x+ ),
),
即x+y﹣7=0和3x﹣y﹣22=0.

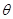 =30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小
=30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小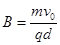 ,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求: