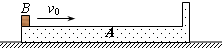
如图所示,长木板A右边固定着一个挡板,包括挡板在内的总质量为1.5M,静止在光滑的水平地面上.小木块B质量为M,从A的左端开始以初速度v0在A上滑动,滑到右端与档板发生碰撞,已知碰撞过程时间极短,碰后木块B恰好滑到A端就停止滑动,已知B与A间的动摩擦因数为μ,B在A板上单程滑行长度为l,求:
(1)碰撞过程中系统损失的机械能;
(2)若μ=,在B与挡板碰撞后的运动过程中,摩擦力对木板A做多少功?
(1)设A、B相对静止后的共同速度为v,整个过程A、B组成的系统动量守恒:
Mv0=(M+M)v
v=v0
由能量守恒得:Q=-(M+1.5M)v2-μMg?2l
联立解得:Q=M-2μMgl
(2)B与A碰撞后,B相对于A向左运动,A所受摩擦力方向向左,A的运动方向向右,故摩擦力做负功.
设B与A碰撞后的瞬间A的速度为v1,B的速度为v2,碰撞后直至相对静止的过程中,系统动量守恒,机械能的减少量等于系统克服摩擦力做的功.即
Mv0=Mv2+1.5Mv1
×1.5M+M-×2.5Mv2=μMgl
可解出v1=v0
这段过程中,A克服摩擦力做功
W=×1.5M-×1.5Mv2=M
答:(1)碰撞过程中系统损失的机械能是M-2μMgl;
(2)若μ=,在B与挡板碰撞后的运动过程中,摩擦力对木板A做功是M.