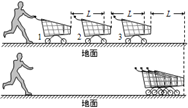
（1）设运动过程中摩擦阻力做的总功为W，则W=-kmgL-2kmgL-3kmgL=-6kmgL；

即整个过程中摩擦阻力所做的总功为-6kmgL．

（2）设第一车初速度为u₀，第一次碰前速度为v₁，碰后共同速度为u₁；第二次碰前速度为v₂，碰后共同速度为u₂；人给第一车的水平冲量大小为I．

由动能定理，对三段减速过程列式

-kmgL=

1

2

m

v

21

-

1

2

m

u

20

-2kmgL=

1

2

(2m)

v

22

-

1

2

(2m)

u

21

-3kmgL=0-

1

2

(3m)

u

22

由动量守恒定律对两次碰撞过程列式

mv₁=2mu₁

2mv₂=3mu₂

人推车过程，由动量定理列式

I=mu₀-0

联立以上六式，解得：I=2m

7kgL

即人给第一辆车水平冲量的大小为2m

7kgL

．

（3）设两次碰撞中系统动能损失分别为△E_k1和△E_k2

△E_k1=

1

2

（2m）u₁²-

1

2

mv₁²=

13

2

kmgL

△E_k2═

1

2

（3m）u₂²-

1

2

（2m）v₂²=

3

2

kmgL

因而

△Ek1

△Ek2

=

13

3

即第一次与第二次碰撞系统功能损失之比为13：3．