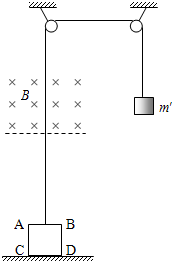
如图所示,正方形导线框ABCD之边长l=10cm,质量m=50g,电阻R=0.1Ω.让线框立在地面上,钩码质量m′=70g,用不可伸长的细线绕过两个定滑轮,连接线框AB边的中点和钩码,线框上方某一高度以上有匀强磁场B=1.0T.当钩码由图示位置被静止释放后,线框即被拉起,上升到AB边进入磁场时就作匀速运动.细绳质量、绳与滑轮间的摩擦和空气阻力均不计,g取10m/s2,求:
(1)线框匀速进入磁场时其中的电流.
(2)线框全部进入磁场所用的时间.
(3)在线框匀速进入磁场的过程中线框产生的电能占钩码损失的机械能的百分比.
(4)线框从图示位置到AB边恰好进入磁场时上升的高度.
(1)安培力:FA=BIL
当物体匀速运动时,由共点力的平衡可知:
m'g=mg+FA
电流I=
=2A;m′g-mg BL
线框匀速进入磁场时其中的电流为2A;
(2)由闭合电路欧姆定律可知:
I=
=E R BLV R
解得V=
=2m/s;IR BL
故线框全部进入的时间t=
=0.05s; l V
(3)因匀速运动过程中动能不变,钩码损失的机械能转化为导线框增加的机械能和导线框中的电能;而线框上升的高度等于钩码下降的高度,故机械能的变化量之比等于两物体的质量之比;
△E′=△E+E电;
=1-E电 △E′
=1-△E E电
=5 7
=28.6%2 7
即线框匀速进入磁场的过程中线框产生的电能占钩码损失的机械能的28.6%;
(4)设高度为h
由机械能守恒可得:
m'gh-mgh=
(m+m')v2;1 2
解得h=1.2m
AB边恰好进入磁场时上升的高度为1.2m.

