问题
解答题
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”. (1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可) 表1.
表2.
|
答案
解:(1)根据题意得:
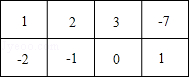 改变第4列
改变第4列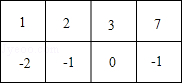 改变第2行
改变第2行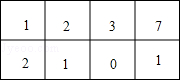
(2)a=1
分析:(1)根据某一行(或某一列)各数之和为负数,则改变改行(或该列)中所有数的符号,称为一次“操作”,先改变表1的第4列,再改变第2行即可;
(2)根据每一列所有数之和分别为2,0,﹣2,0,每一行所有数之和分别为﹣1,1,然后分别根据如果操作第三列或第一行,根据每行的各数之和与每列的各数之和均为非负整数,列出不等式组,求出不等式组的解集,即可得出答案。
解:(1)根据题意得:
 改变第4列
改变第4列 改变第2行
改变第2行
(2)∵每一列所有数之和分别为2,0,﹣2,0,每一行所有数之和分别为﹣1,1,
∴①如果操作第三列,为:
| a | a2﹣1 | a | ﹣a2 |
| 2﹣a | 1﹣a2 | 2﹣a | a2 |
由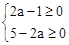 解得:
解得: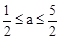 ,
,
又∵a为整数,∴a=1或a=2。
②如果操作第一行,为:
| ﹣a | 1﹣a2 | a | a2 |
| 2﹣a | 1﹣a2 | a﹣2 | a2 |
由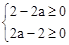 解得:a=1。
解得:a=1。
此时2﹣2a2=0,2a2=2,
综上可知:a=1。
