问题
问答题
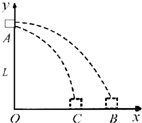
如为俯视图,在一光滑水平面上建立x-y平面直角坐标系.有一质量为m的小木块从A点沿x轴方向以某初速度射出,A点离x轴距离为L,小木块沿y轴负方向始终受到恒力F1=F0.小木块的运动轨迹与x轴的交点B到y轴距离为S;当同时施加沿x轴负方向恒力F2时,小木块仍以原来初速度射出,其运动轨迹与x轴的交点C到y轴距离为
S.不计空气阻力.3 4
(1)求小木块初速度v0的大小;
(2)恒力F2的大小;
(3)若F2=-kv,v为小木块的速度.仍以原来的初速度射出小木块,发现小木块垂直x轴匀速通过.求此过程中F2对小木块所做的功.
答案
(1)分析A到B过程
由类平抛得:
竖直方向:L=1 2
t2①F0 m
水平方向:s=v0t②
由①②解方程得v0=sF0 2Lm
(2)设小木块到x轴时沿x轴方向上的速度为vx
分析x轴,由匀变速直线运动的规律得:
vx=v0-
tF2 m
即
s=3 4
t③v0+vt 2
又因为L=1 2
t2④F0 m
联立③④解得F2=F0S 4L
(3)匀速时F2=-kvt
分析A到C过程由动能定理得:F0L+W3=
m1 2 v 2t
解得:W3=1 2
-F0LmF22 k2
答:(1)小木块初速度v0的为s
;F0 2Lm
(2)恒力F2的大小为
;F0S 4L
(3)此过程中F2对小木块所做的功为1 2
-F0L.mF22 k2