问题
问答题
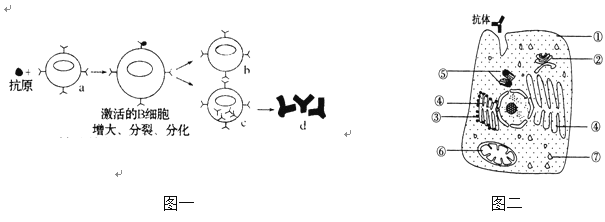
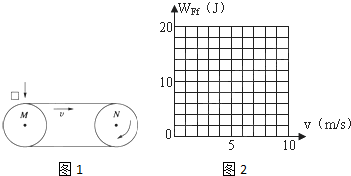
如图1所示，水平的传送带以速度v=4m/s顺时针运转，两传动轮M、N之间的距离为L=9m，若在M轮的正上方，将一质量为m=1kg的物体轻放在传送带上，已知物体与传送带之间的动摩擦因数μ=0.2，g取10m/s2，在物体由M处传送到N处的过程中，则
（1）物体从M到N经历的时间为多少？物体克服摩擦力做功为多少？
（2）若传送带以不同速度v顺时针运转，在图2中画出物体克服摩擦力做功WFf与v的关系图象？（只要求作出图象即可）
答案
（1）设运行过程中货物的加速度为a，根据牛顿第二定律得：
μmg=ma
解得：a=μg=0.2×10=m/s2=2m/s2
加速到与带同速用时：t1=
=V a
=2s4 2
此时位移：S1=1 2
=at 21
×2×4=4m1 2
剩下的位移L-S1=Vt2，得：t2=
=1.25s5 4
物体从M到N经历的时间为t=2+1.25=3.25s
根据动能定理，摩擦力做功W=
mV2=8J，即传送带对物体的摩擦力做功为8J．1 2
（2）若物体一直加速到N端时，速度为V′=
=2aL
=6m/s2×2×9
当传送带的速度v≤6m/s：WFf=
mv2=1 2 v2 2
当传送带的速度v＞6m/s：WFf=
=18J62 2
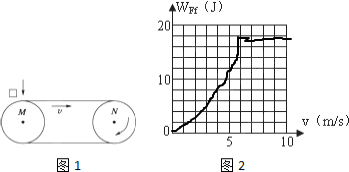
物体克服摩擦力做功WFf与v的关系图象如图：
答：（1）物体从M到N经历的时间为3.25s，物体克服摩擦力做功为8J；
（2）如图