设f(x)在区间[a,b]上连续,且f(x)>0,
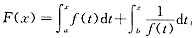 ,证明:
,证明:
(Ⅰ)方程F(x)=0在(a,b)内有唯一实根;
(Ⅱ)函数|F(x)|在(a,b)内有且仅有一个不可导的点.
参考答案:
[分析]: (1)利用连续函数零点定理证明根的存在性,利用单调性证明根的唯一性.
(2)由于f(x)连续且f(x)>0,则F(x)处处可导.而|F(x)|与F(x)的可导性有何关系呢
[证] 1)显然[*]是[a,b]上的连续函数,由于
[*]
由连续函数零点定理知,F(x)在(a,b)内至少有一个零点,又
[*]
则F(x)在[a,b]上单调增,从而F(x)在(a,b)内最多一个零点.
故方程F(x)=0在(a,b)有唯一实根.
2)不妨设F(x)在区间(a,b)内的唯一零点为x0,以下证明F(x)在(a,b)内仅.在x0点不可导,其余点都可导.事实上,由前面讨论知
F(x0)=0,F′(x0)>0
令[*],则
[*]
[*],则
[*]在x0处不可导,即|F(x)|在x0处不可导.
若x1≠x0,且x1∈(a,b),则
F(x1)≠0
不妨设F(x1)>0,由于F(x)连续,则存在x1的邻域,在此邻域内F(x)>o,从而在此邻域内
|F(x)|=F(x)
由于F(x)在点x1处可导,则|F(x)|在x1处可导.这说明|F(x)|在(a,b)内除x0点外处处可导.
故|F(x)|在(a,b)内有且仅有一个不可导的点.
[评注] 由本题2)的证明可得到关于f(x)和|f(x)|可导性之间的关系.结论是设f(x)在(a,b)内连续,则在(a,b)内使函数值f(x)不为零的点上,函数f(x)与|f(x)|可导性相同,而在函数值f(x)为零的点上,f(x)与|f(x)|的可导性不完全相同,关于此问题有以下结论:
1)若f(x0)=0,且f′(x0)≠0,则|f(x)|在x0处不可导(本题中已证明);
2)若f(x0)=0,且f′(x0)=0,则|f(x)|在x0处可导(请读者证明);
3)若f(x0)=0,且f(x)在x0点不可导,则|f(x)|在x0点一定不可导(请读者证明).
以上结论在处理有关f(x)和|f(x)|的可导性的问题时会给我们带来很多方便.tu/1212/yjs/ky/s1279.18A2E76.jpgtu/1212/yjs/ky/s1279.18A7D32.jpgtu/1212/yjs/ky/s1279.18B2A79.jpgtu/1212/yjs/ky/s1279.18CA3AC.jpgtu/1212/yjs/ky/s1279.18D109E.jpgtu/1212/yjs/ky/s1279.18D5EED.jpgtu/1212/yjs/ky/s1279.18DC885.jpg
