设f(x)和g(x)在[0,1]上连续,在(0,1)内可导,f(0)=f(1)=-1.
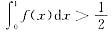 ,试证至少存在一点e∈(0,1)使,
,试证至少存在一点e∈(0,1)使,
f′(ξ)+g′(ξ)[f(ξ)-ξ]=1.
参考答案:
[分析]: 此类问题一般都需构造辅助函数,然后用罗尔定理.
要证f′(ξ)+g′(ξ)[f(ξ)-ξ]=1,即要证
[f′(ξ)-1]+g′(ξ)[f(ξ)-ξ]=0.
为此,可令F(x)=(f(x)-x)eg(x),
此时 F′(x)=eg(x){[f′(x)-1]+g′(x)[f(x)-x]}
[证] 令F(x)=(f(x)-x)eg(x),则
F(0)=-eg(0)<0,F(1)=-2eg(1)<0,
又[*]
由积分中值定理知,至少存在一点c∈(0,1),使
f(c)-c>0
即 F(c)>0.
由连续函数的零点定理知:
存在点a∈(0,c),使F(a)=0,
存在点b∈(c,1),使F(b)=0,
则F(z)在区间[a,b]上满足罗尔定理条件,由罗尔定理知,至少存在一点ξ∈(a,b),使
F′(ξ)=0
即eg(ξ){[f′(ξ)-1]+g′(ξ)[f′(ξ)-ξ]}=0
但eg(ξ)≠0
则[f′(ξ)-1]+g′(ξ)[f(ξ)-ξ]=0
故至少存在一点ξ∈(0,1),使
f′(ξ)+g′(ξ)[f(ξ)-ξ]=1.
[评注] 本题的关键在于构造辅助函数.如果要证明至少存在一点ξ∈(a,b),使
f′(ξ)+g′(ξ)f(ξ)=0
可构造辅助函数 F(x)=eg(x)f(x)
此时,F′(x)=eg(x)[f′(x)+g′(x)f(x)]这代表了一类比较常见的辅助函数,特别的要证至少存在一点ξ∈(a,b),使
f′(ξ)+λf(ξ)=0(λ为实数)
即g′(x)=λ,可取g(x)=λx
F(x)=eλxf(x).tu/1212/yjs/ky/s1279.1A47EBA.jpg
