问题
解答题
已知直线方程为（2+m）x+（1﹣2m）y+4﹣3m=0．
（Ⅰ）若直线不经过第一象限，求m的范围；
（Ⅱ）若直线分别与x轴、y轴的负半轴交于A，B两点，
求△AOB面积的最小值及此时直线的方程．
答案
解：（Ⅰ） （法一）①1﹣2m=0，即m=
时，x=1，不过第一象限，∴m=
．
②1﹣2m≠0，即m≠
时，
y=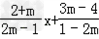
，
∴
，
∴
，
∴﹣
．
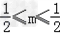（法二）解：（2+m）x+（1﹣2m）y+4﹣3m=0化为（x﹣2y﹣3）m=﹣2x﹣y﹣4．
由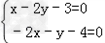
得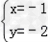 
，
∴直线必过定点（﹣1，﹣2）．
∴1﹣2m=0或者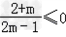
，
∴﹣
．
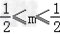（Ⅱ）解：设直线的斜率为k（k＜0），则其方程为y+2=k（x+1），
∴OA=|
﹣1|，OB=|k﹣2|，
S△AOB=
OAOB=
|（
﹣1）（k﹣2）|=
|﹣
|
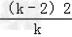∵k＜0，∴﹣k＞0，
∴S△AOB=
[﹣
]=
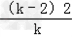[4+（﹣
）+（﹣k）]≥4．
当且仅当﹣
=﹣k，即k=﹣2时取等号．
∴△AOB的面积最小值是4，
直线的方程为y+2=﹣2（x+1），即y+2x+4=0．