问题
解答题
和谐商场销售甲，乙两种商品，甲钟商品每件进价15元，售价20元；乙种商品每件进价35元，售价45元。
（1）若该商场同时购进甲，乙两种商品共100件，恰好用去2700元，求能购进甲，乙两种商品各多少件？
（2）该商场为使甲，乙两种商品共100件的总利润（利润=售价—进价）不少于750元，且不超过760元，请你帮助该商场设计相应的进货方案。
答案
（1）商场购进甲种商品40件，乙种商品60件．（2）方案一：购进甲种商品48件，购进乙种商品52件．方案二：购进甲种商品49件，购进乙种商品51件．方案三：购进甲种商品50件，购进乙种商品50件．
题目分析：（1）首先设出购进甲商品的件数，然后根据“同时购进甲、乙两种商品共100件”表示出购进乙商品的件数；然后根据“恰好用去2700元”列方程求出未知数的值，即可得解．
（2）此题可根据“甲、乙两种商品共100件的总利润不少于750元，且不超过760元”列不等式组来求解．
试题解析：（1）设该商场购进甲种商品x件，根据题意可得：15x+35（100-x）=2700，（2分）
解得：x=40；
乙种商品：100-40=60（件），
答：该商场购进甲种商品40件，乙种商品60件．
（2）设该商场购进甲种商品a件，则购进乙种商品（100-a）件，根据题意得：
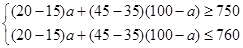
解得：48≤a≤50；（7分）
∵a是正整数，
∴a=48或a=49或a=50；
∴进货方案有三种：
方案一：购进甲种商品48件，购进乙种商品52件．
方案二：购进甲种商品49件，购进乙种商品51件．
方案三：购进甲种商品50件，购进乙种商品50件．
主不能阻挠俄国同欧洲商品交易的增长，不能保持住旧的崩溃的经济形态。如克里木（克里米亚）战争显示出农奴制俄国的腐败和无能。解放以前农民的“叛乱”每十年都要高涨一次。这使头号大地主亚历山大二世不得不承认，从上面解放比等待下面推翻要好些。