问题
填空题
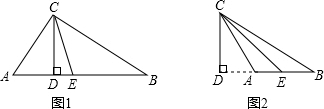
在△ABC中,CD为高,且AD=2,BD=8,如果CD=4,那么∠ACB的平分线CE=______.
答案
∵在Rt△ACD中,AC=
=AD2+CD2
=222+42
,5
在Rt△BCD中,BC=
=BD2+CD2
=482+42
,5
∵CE是△ABC的角平分线,
∴AE:BE=AC:BC=2
:45
=1:2,5
①如图1,∠A是锐角时,AB=AD+BD=2+8=10,
∴AE=
×10=1 1+2
,10 3
DE=AE-AD=
-2=10 3
,4 3
在Rt△CDE中,CE=
=CD2+DE2
=42+(
)24 3
,4 10 3
②如图2,∠A是钝角时,AB=BD-AD=8-2=6,
∴AE=
×6=2,1 1+2
DE=AE+AD=2+2=4,
在Rt△CDE中,CE=
=CD2+DE2
=442+42
,2
综上所述,CE的长是
或44 10 3
.2
故答案为:
或44 10 3
.2