如图所示,半径为R的光滑半圆轨道ABC与倾角为θ=37°的粗糙斜面轨道DC相切于C,圆轨道的直径AC与斜面垂直.质量为m的小球从A点左上方距A高为h的斜面上方P点以某一速度水平抛出,刚好与半圆轨道的A点相切进入半圆轨道内侧,之后经半圆轨道沿斜面刚好滑到与抛出点等高的D处.已知当地的重力加速度为g,取R=
h,sin37°=0.6,cos37°=0.8,不计空气阻力,求:50 9
(1)小球被抛出时的速度v0;
(2)小球到达半圆轨道最低点B时,对轨道的压力大小;
(3)小球从C到D过程中摩擦力做的功W.
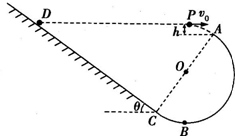

(1)小球到达A点时,速度与水平方向的夹角为θ,如图所示.
则有
=2gh ①v 21
由几何关系得 v0=v1cotθ ②
得 v0=4 3
③2gh
(2)A、B间竖直高度H=R(1+cosθ)④
设小球到达B点时的速度为v,则从抛出点到B过程中,根据机械能守恒有
m1 2
+mg(H+h)=v 20
mv2 ⑤1 2
在B点,有 FN-mg=m
⑥v2 R
联立解得 FN=5.6mg⑦
由牛顿第三定律知,小球在B点对轨道的压力大小是FN′=FN=5.6mg,方向竖直向下. ⑧
(3)整个运动知过程中,重力做功为零,根据动能定理得知:小球沿斜面上滑过程中摩擦力做的功等于小球做平抛运动的初动能,有
W=
m1 2
=v 20
mgh ⑨16 9
答:(1)小球被抛出时的速度v0是4 3
.2gh
(2)小球到达半圆轨道最低点B时,对轨道的压力大小是5.6mg,方向竖直向下.
(3)小球从C到D过程中摩擦力做的功W是
mgh.16 9
