搜题请搜索小程序“爱下问搜题”
问题 填空题

过点P（5，4）作直线l与圆O：x2+y2=25交于A，B两点，若PA=2，则直线l的方程为______．

答案

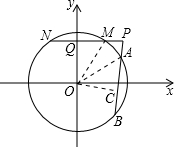
当直线l斜率为0时，A与M重合，B与N重合，此时OQ=4，

由垂径定理定理得到Q为MN中点，连接OM，

根据勾股定理得：QM=

OM2-OQ2
=3，

∴MN=2QM=6，

此时直线l方程为y=4，符合题意；

当直线l斜率不为0时，设为k，直线l方程为y-4=k（x-5），即kx-y+4-5k=0，

由割线定理得到AB=MN=6，再由垂径定理得到C为AB的中点，即AC=

1
2
AB=3，

过O作OC⊥AB，连接OA，

根据勾股定理得：OC=

OA2-AC2
=4，

∴圆心O到直线l的距离d=

|4-5k|
1+k2
=4，解得：k=0（舍去）或k=
40
9
，

则此时直线l的方程为

40
9
x-y+4-5×
40
9
=0，即40x-9y-164=0，

综上，直线l的方程为y=4或40x-9y-164=0．

故答案为：y=4或40x-9y-164=0

材料题

阅读材料，回答问题：

相传，尧年老时，征求各部落首领的意见，推举舜做他的继承人，舜年老后，采用同样的办法把位置让给禹。

（1）材料反映的是什么制度？

_______________________________________________________

（2）这一制度的实质是什么？

_______________________________________________________

（3）这一制度是怎样结束的？

_______________________________________________________
查看答案
阅读理解与欣赏

课内阅读。

　　她以为，水一定都洒了，但是没有，罐子端端正正地在地上放着，罐子里的水还是满满的。小姑娘往手掌里倒了一点儿水，小狗把它舔净了，变得欢喜起来。当小姑娘再拿水罐时，木头做的水罐竟变成了银的。小姑娘回到家，把水罐交给了母亲。母亲说：“我反正要死了，还是你自己喝吧。”她又把水罐递给小姑娘。就在这一瞬间，水罐又变成了金的。这时，小姑娘再也忍不住，正想凑上水罐去喝口水的时候，突然从门外进来一个过路人讨水喝。小姑娘咽了一口唾沫，把水罐递给了这个过路人。这时突然从水罐里跳出了七颗很大的钻石，接着从里面涌出了一股巨大的清澈又新鲜的水流。那七颗钻石越升越高，升到了天上，变成了七颗星星。

1.第1自然段中第一个“这时”是指______，第二个“这时”是指________。

2．什么时候水罐变成了银的？

_______________________________________

_______________________________________

3．什么时候水罐变成了金的？

________________________________________

________________________________________

4．什么时候水罐里跳出钻石并涌出水流？

_______________________________________

_______________________________________

5．你觉得文中的小姑娘是个怎样的人？为什么故事的结局会如此美好？请联系文章内容谈谈你的感悟。

_________________________________________

_________________________________________
查看答案