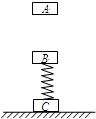
如图所示,物体B和物体C用劲度系数为k的轻弹簧连接并竖直地静置于水平地面上.将一个物体A从物体B的正上方距离B的高度为H0处由静止释放,下落后与物体B碰撞,碰撞后A与B粘合在一起并立刻向下运动,在以后的运动中A、B不再分离.已知物体A、B、C的质量均为M,重力加速度为g,忽略空气阻力.
(1)求A与B碰撞后瞬间的速度大小.
(2)A和B一起运动达到最大速度时,物体C对水平地面的压力为多大?
(3)开始时,物体A从距B多大的高度自由落下时,在以后的运动中才能使物体C恰好离开地面?
(1)设物体A碰前速度为v1,对物体A从H0高度处自由下落,
由机械能守恒定律得:MgH0=
Mv12,解得:v1=1 2
.2gH0
设A、B碰撞后共同速度为v2,则由动量守恒定律得:
Mv1=2Mv2,v2=
.gH0 2
(2)当A、B达到最大速度时,A、B所受合外力为零,设此时弹力为F,对A、B由平衡条件得,F=2Mg.
设地面对C的支持力为N,对ABC整体,因加速度为零,所以N=3Mg.
由牛顿第三定律得C对地面的压力大小为N′=3Mg.
(3)设物体A从距B的高度H处自由落下,根据(1)的结果,
A、B碰撞后共同速度v2=
.gH 2
当C刚好离开地面时,由胡克定律得弹簧伸长量为X=
.Mg k
根据对称性,当A、B一起上升到弹簧伸长为X时弹簧的势能与A、B碰撞后瞬间的势能相等.
则对A、B一起运动到C刚好离开地面的过程中,由机械能守恒得:
×2Mv22=4MgX,1 2
联立以上方程解得:H=
.8Mg k
答:(1)A与B碰撞后瞬间的速度大小为
.2gH0
(2)A和B一起运动达到最大速度时,物体C对水平地面的压力为3Mg.
(3)开始时,物体A从距B
的高度自由落下时,在以后的运动中才能使物体C恰好离开地面.8Mg k
