问题
计算题
【选修3-4选做题】
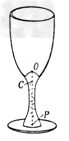
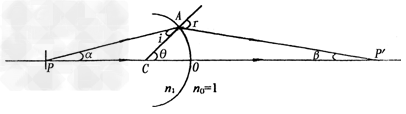
有一种高脚酒杯（脚高且细），如图所示，杯内底面为一凸起的球面，球心在顶点O下方玻璃中的C点，球面的半径为R=1.50cm，O点到杯口平面的距离为8.0cm，在杯脚底中心处P点紧贴一张小画片，P点距O点6.3cm．这种酒杯未斟酒水，若在杯口上方向杯底方向观看，看不出画片上的景物．已知玻璃的折射率n=1.56，角度很小时，可以认为sinα=α。求：
(1)光在玻璃中的传播速度；
(2)计算画片成像位置离杯口的距离．
答案
解：（1）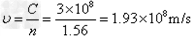
（2）把酒杯放平，分析成像问题，未斟酒时，杯底凸球面的两侧介质的折射率分别为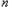
和
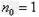。在图中，P为画片中心，由P发出经过球心C的光线PO经过顶点不变方向进入空气中；由P发出的与PO成角的另一光线PA在A处折射。设A处入射角为i，折射角为r，半径CA与PO的夹有为θ，由折射定律和几何关系可得
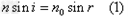
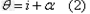
在△PAC中，由正弦定理，有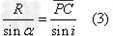
考虑近轴光线成像，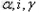
都是小角度，则有
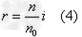
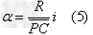
由(2)(4)(5)式、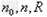
的数值及
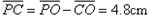，可得
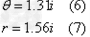
由(6)(7)式有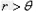
由上式及图可知，折射线将与PO延长线相交于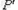
，
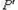即为P点的实像，画面将成实像于
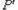处
在△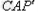
中，由正弦定理有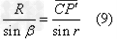
又有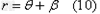
考虑到是近轴光线，由(9)(10)式可得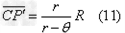
又有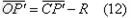
由以上各式并代入数据，可得
所以像离杯口的距离为0.1cm