问题
计算题
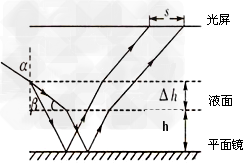
如图所示是一种液体深度自动监测仪示意图，在容器的底部水平放置一平面镜，在平面镜上方有一光屏与平面镜平行．激光器发出的一束光线以60°的入射角射到液面上，进入液体中的光线经平面镜反射后再从液体的上表面射出，打在光屏上形成一亮点，液体的深度变化后光屏上亮点向左移动了2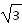
dm，已知该液体的折射率n=
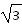．真空中光速c=3.0×108 m/s，不考虑经液面反射的光线。求：
（1）光在该液体中传播速度的大小；
（2）液面高度的变化量；
（3）液体的深度变化前后激光从发出到打到光屏上的时间变化了多少？
答案
解：设入射角为α，折射角为β，原来液面深度为h，液面深度增加△h，屏上光点移动的距离 s=2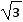
dm，n=
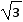，c=3.0×108 m/s，α=60°
（1）光在该液体中的传播速度为：v=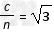
×108 m/s
（2）光路图如图所示
根据折射定律n=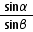
，得β=30°
由几何关系得2htanβ+2△htanα=2(△h+h)tanβ+s
△h=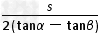
=1.5 dm
（3）液体的深度变化前后激光从发出到打到光屏上的时间变化为
△t=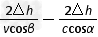
=0