问题
计算题
（10分）如图，粗糙水平地面上有一压缩并锁定的弹簧，弹簧左端固定于竖直墙壁上，右端与一质量为m=0.1kg的小物块A（可视为质点）接触但不连接，光滑的固定半圆周轨道MP与地面相切于M点，P点为轨道的最高点。现解除弹簧锁定，弹簧将小物块A推出，A沿粗糙水平地面运动，之后沿圆周轨道运动并恰能通过P点。已知A与地面间的动摩擦因数为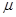
=0.25，最初A与M点的距离L1="2m" , 圆周轨道半径R=0.4m，g取10m/s2，空气阻力不计。求：
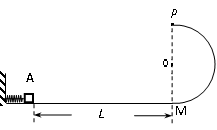
(1)小滑块到达P点时的速度大小；
(2)弹簧弹力对滑块所做的功。
(3)弹簧仍将小物块从A点推出，为了使小物块能够从P点落回A点，此时A与M点的距离L2应该取多大。
答案
（1）2m/s；（2）1.55m
题目分析：（1）设小物块A到达圆周轨道最高点P时的速度为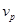
,
由题意有：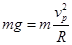
解得：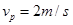
（2）从解除锁定到物块滑至最高点P的过程中，由动能定理有：
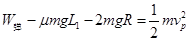
解得：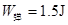
（3）小球离开P点以v0做平抛，落地的时间为t，
根据：
解得：t=0.4s
L2＝v0t
从解除锁定到物块滑至最高点P的过程中，由动能定理有：
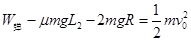
解得：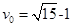
≈2.87m/s
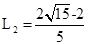≈1.55m