问题
问答题
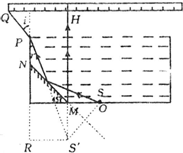
如图所示,一不透明的圆柱形容器内装满折射率n=
的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底边半径为(1+2
)dm,OM=1dm,在容器中央正上方1dm 处水平放置一足够长的刻度尺,求光源 S 发出的光线经平面镜反射后,照射到刻度尺的长度.(不考虑容器侧壁和液面的反射)3
答案
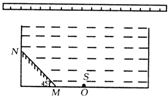
设容器高为H.作图找出发光点S在平面镜中的像点S′,连接SM延长交直尺于H点.
由题:光线SM的入射角为45°,根据反射定律可知反射角等于45°,则MH沿竖直方向.
连接S′P,根据对称性得 S′M=OM=1m,则在Rt△PR S′中,R S′=
dm,PR=H+S′M=3dm 3
由几何知识得∠r=30°.
根据折射定律可得:n=sini sinr
解得sini=
,∠i=45°,2 2
故刻度尺上被照亮的范围QH=1dm+
dm=(1+3
)dm3
答:刻度尺上被照亮的范围QH=1dm+
dm=(1+3
)dm.3