问题
问答题
如图所示,半圆玻璃砖的半径R=9cm,折射率为n=
,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.(已知sinC=3
,C为光线从玻璃进入空气发生全反射的临界角)1 n
(1)作出光路图(不考虑光沿原路返回);
(2)求两个光斑之间的距离;
(3)改变入射角,使屏MN上只剩一个光斑,求此光斑离A点的最长距离.

答案
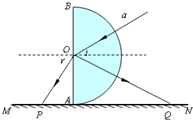
解析:(1)光路图如图所示.
(2)设折射角为r,根据折射定律和光路的可逆性可得:
n=
=sinr sini
,sinr sin30°
解得:r=60°,
由几何知识得△OPQ为直角三角形,
所以两个光斑PQ之间的距离为:
PQ=PA+AQ=Rtan30°+Rtan60°=12
cm.3
(3)入射角增大的过程中,当发生全反射时屏MN上只剩一个光斑,此光斑离A最远时,恰好发生全反射,入射角等于临界角:
i=C,则有:sinC=
,1 n
代入数据解得:
Q′A=
=9R tanC
cm.2
答:(1)光路图如右图所示.
(2)两个光斑之间的距离为12
cm.3
(3)改变入射角,使屏MN上只剩一个光斑,则此光斑离A点的最长距离为9
cm.2
