问题
问答题
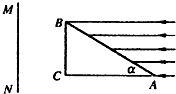
如图所示，一个横截面为直角三角形的三棱镜，∠A=30°，∠C=90°，BC边的长为L．一个大光屏MN与BC平行，到BC的距离也是L．三棱镜材料的折射率是n=
．一束平行光平行于AC方向射到三棱镜的 AB面上．求：3
（1）用作图法画出光屏上被照亮的部分，并求被照亮部分的宽度．
（2）光屏移动到什么位置才能消除两个照亮部分之间的阴影区？
答案
（1）作出光路图如图所示．
平行光线进入三棱镜后被CD分成两部分，BD部分的光线直接经BC折射后，射到光屏上，AD部分在AC面上发生全反射，再经BC面折射后射到屏上．
在AB面上：入射角i=60°，由n=
得：r=30°sini sinr
对于BD部分：光线射到BC面上入射角为i′=30°，由光路可逆性得知，折射角r′=60′，由几何知识得知NN′=L
对于AD部分：光线射到AC面上，入射角为i″=60°．
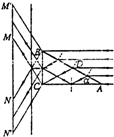
设临界角为C，则sinC=
=1 n
＜sin60°，故C＜60°，则光线在AC面上发生全反射．1 3
根据几何关系得知：MM′=L．
故被照亮部分的宽度为2L．
（2）根据光路图可知，将屏向右移到图中虚线位置，能消除两个照亮部分之间的阴影区．
由几何知识和屏到BC边的距离得知，屏到BC距离为
L．3 6
答：
（1）用作图法画出光屏上被照亮的部分如图所示，被照亮部分的宽度为2L．
（2）光屏移动到距离BC
L的位置才能消除两个照亮部分之间的阴影区．3 6