问题
填空题
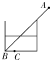
如图所示,一储油圆桶,底面直径与桶高均为d.当桶内无油时,从某点恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高的一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距
,由此可得油的折射率n=______;光在油中传播的速度______m/s.(结果可用根式表示)d 4
答案
由题意得,光线在油中的入射角的正弦sinβ=
=d 4
)2(
)2+(d 4 d 2
,光线在空气中折射角的正弦sinα=5 5
=d 2 (
)2+(d 2
)2d 2
.2 2
则折射率n=
=sinα sinβ
.10 2
根据v=
得,v=c n
=c n
c.10 5
故答案为:
,10 2
c.10 5
