搜题请搜索小程序“爱下问搜题”
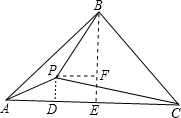
问题 填空题
在等腰直角△ABC中，AB=BC=5，P是△ABC内一点，且PA=
5
，PC=5，则PB=______．
答案

如图所示，过点B作BE⊥AC，过点P作PD，PF分别垂直AC，BE

在△APD中，PA2=PD2+AD2=5，

在△PCD中，PC2=PD2+CD2，且AD+CD=5

2
，

解得AD=

3
2
2
，CD=
7
2
2
，PD=
2
2
，

在Rt△ABC中，BE=AE=

5
2
2
，

所以在Rt△BPF中，PB2=PF2+BF2=

2
2+(
5
2
2
-
2
2
)2=10，

所以PB=

10
．

填空题

把下面的字去掉偏旁部首是什么字并写出读音。

傣(      )              毯(      )          

炮(      )              盛(      )          

查看答案
单项选择题

肝郁气滞型癃闭的主证是

A．小便点滴不通，或量极小而短赤灼热，小腹胀满，口苦口粘，舌质红，苔黄腻，脉沉数
B．小便不畅，或点滴不通，咽干，烦渴欲饮，呼吸急促，舌苔薄黄，脉数
C．小腹坠胀，时欲小便而不得出，或量少而不爽利，精神疲乏，食欲不振，气短而语声低细，舌质淡，苔薄，脉象沉弱
D．情志忧郁，或多烦善怒，小便不通，或通而不爽，胁腹胀满，舌红，苔薄或黄，脉弦
E．小便不通或点滴不爽，排出无力，面色白，神气怯弱，腰膝冷而酸软无力，舌质淡，脉沉细而尺弱

查看答案