问题
填空题
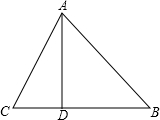
已知在△ABC中，AB=4，AC=3，BC边上的高等于2.4，则△ABC的周长=______．
答案
①当∠C为锐角：
作AD⊥BC于D，则AD为BC边上的高，AD=2.4，如下图所示：
在Rt△ADC中，由勾股定理得：
AC2=AD2+DC2，
∴DC=
=AC2-AD2
=1.8，32-2.42
在Rt△ADB中，由勾股定理得：
AB2=AD2+BD2，
∴BD=
=AB2-AD2
=3.2，42-2.42
∴BC=BD+DC=3.2+1.8=5，
所以，△ABC的周长为AB+AC+BC=4+3+5=12．
②当∠C为钝角：
作AD⊥BC，交BC的延长线于D，则AD为BC边上的高，AD=12，
如图所示：在Rt△ADC中，由勾股定理得：
AC2=AD2+DC2，
∴DC=
=AC2-AD2
=1.8，32-2.42
在Rt△ADB中，由勾股定理得：
AB2=AD2+BD2，
∴BD=
=AB2-AD2
=3.2，42-2.42
∴BC=BD-DC=3.2-1.8=1.4，
所以，△ABC的周长为AB+AC+BC=4+3+1.4=8.4．
故△ABC的周长为12或8.4．
故答案为：12或8.4．
