问题
问答题
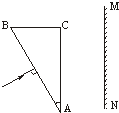
如图所示,横截面是直角三角形ABC的三棱镜对红光的折射率为n1,对紫光的折射率为n2.一束很细的白光由棱镜的一个侧面AB垂直射入,从另一个侧面AC折射出来.已知棱镜的顶角∠A=30°,AC边平行于光屏MN,且与光屏的距离为L.求在光屏上得到的可见光谱的宽度.
答案
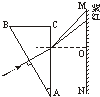
光路如图所示.设射到屏上的红光和紫光偏离O点的距离分别
为d1和d2,折射角分别为θ2和θ3,入射角θ1=30°,则由折射定律
=1 n1 sinθ1 sinθ2
=1 n2 sinθ1 sinθ3
得sinθ2=n1sinθ1=
n11 2
sinθ3=n2sinθ1=
n21 2
则d1=Ltanθ2=Ln1 4-n12
d2=Ltanθ3=Ln2 4-n22
则可见光谱的宽度为
d2-d1=L(
-n2 4-n22
).n1 4-n12
答:光屏上得到的可见光谱的宽度为L(
-n2 4-n22
).n1 4-n12
