问题
问答题
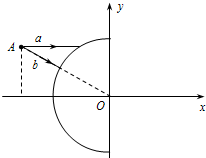
如图所示,半径为R的半圆柱形玻璃砖,放置在直角坐标系xOy中,圆心与坐标系原点O重合.在第二象限中坐标为(-1.5R,
R)的点A处,放置一个激光器(图中未画出),发出的两束细激光束a和b,其中,激光束a平行于x轴射向玻璃砖,激光束b沿AO方向射向玻璃砖.已知激光在玻璃砖中的折射率为3 2
.3
(1)作出光束a和b通过玻璃砖的光路图,并证明a和b射出玻璃砖后是否相交;
(2)求出激光束a射出玻璃砖后与x轴交点的坐标.
答案
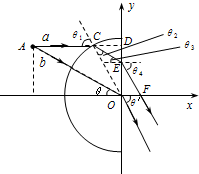
(1)激光束a、b经过玻璃砖的折射光路图如图所示:
如图,tanθ=
=
R3 2 1.5R
得θ=30°3 3
激光束b:
在O点有:n=
得 θ′=60°sinθ sinθ′
又 sinθ1=
=
R3 2 R
得 θ1=60°3 2
激光束a,在C点有:n=
得 θ2=30°sinθ1 sinθ2
在E点 n=
=sinθ4 sinθ3
得 θ4=60°sinθ4 sin(θ1-θ2)
由θ4=θ′,两束光射出后应平行,故不相交.
(2)在△CDO中,CD=Rcosθ1=
R1 2
在△CDE中,DE=CDtan(θ1-θ2)=
R3 6
在△EFO中,OF=OEcotθ4=(
R-3 2
R)3 6
=3 3
R1 3
所以,光束a射出玻璃砖后与x轴交点的坐标为(
R,0)1 3
答:(1)作出光束a和b通过玻璃砖的光路图如图,证明见上;
(2)光束a射出玻璃砖后与x轴交点的坐标为(
R,0).1 3