问题
问答题
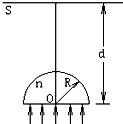
一束截面为圆形(半径为R)的平行单色光正面射向一玻璃半球的平面,如图所示,经折射后在屏S上形成一圆形光斑.已知入射光的波长为λ、功率为P,玻璃半球的半径为R,折射率为n,屏S 到球心O的距离为d(d>3R).
(1)从O点射入玻璃砖的光线要多长时间能到达屏S?
(2)光从圆弧面上什么范围射出?
(3)屏S上光斑的半径为多大?
答案
解(1)光线在玻璃中的时间t1=
=R v1
;光线在空气中的时间t2=R c n
.则从O点射入玻璃砖的光线要能到达屏S的时间t=t1+t2=d-R c
+R c n
=d-R c (n-1)R+d c
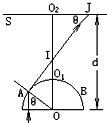
(2)光线从玻璃射入空气,当入射角大于或等于临界角时,则会发生光的全反射现象,
所以临界角θ=arcsin
,光从圆弧AO1B部分出射,1 n
则有∠AOO1=∠BOO1=arcsin
; 1 n
(3)作出光路图,根据几何关系可得:r=O2J=(d-IO)cotθ,
IO=
,R cosθ
解得:r=d
-nR n2-1
答:(1)从O点射入玻璃砖的光线要间t=
时间能到达屏S;(n-1)R+d c
(2)光从圆弧面上AO1B部分范围射出则有∠AOO1=∠BOO1=arcsin
;1 n
(3)屏S上光斑的半径得:r=d
-nR.n2-1
