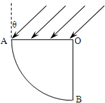
如图,空气中有一折射率为
的玻璃柱体,其横截面是圆心角为90°、半径为R的扇形OAB.一束平行于横截面,以入射角θ照射到OA上,OB不透光.若只考虑首次入射到圆弧AB上的光( )2
A..若θ=45°,则AB上有光透出部分的弧长是5πR 12
B..若θ=45°,则AB上有光透出部分的弧长是πR 4
C..增大θ,则AB上有光透出部分的弧长不变
D..增大θ,则AB上有光透出部分的弧长变大
A、根据折射定律有:
=sin45° sinr
可得光进入玻璃后光线与竖直方向的夹角为30°.2
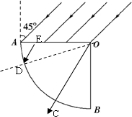
过O的光线垂直入射到AB界面上点C射出,C到B之间没有光线射出;越接近A的光线入射到AB界面上时的入射角越大,发生全反射的可能性越大.
根据临界角公式:sinC=
,得临界角为45°,如果AB界面上的临界点为D,此光线在AO界面上点E入射,在三角形ODE中可求得OD与水平方向的夹角为180°-(120°+45°)=15°,所以A到D之间没有光线射出.由此可得没有光线射出的圆弧对应圆心角为90°-(30°+15°)=45°1 2
所以有光透出的部分的弧长为
.故A错误,B正确.πR 4
C、增大θ,则折射角也增大,根据几何关系,设折射角为α,则有光线射出的部分对应的圆心角为90°-θ-(180°-135°-θ)=45°,知对应的弧长不变.故C正确,D错误.
故选BC.
