如图所示,ABCD是表示折射率为n的透明长方体,其四周介质的折射率均为1,一单色光束以角度θ入射至AB面上的P点,AP=
.AD 2
(1)若要此光束进入长方体后能直接射至AD面上,角θ的最小值是多少?
(2)若要此光束直接射到AD面上能在AD面上全反射,角θ应在什么范围内?
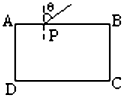
(1)要使光束进入长方体后能射至AD面上,折射光线射到D点时角θ最小,此时折射角也最小,设最小折射角为α,AP=d.如图.
根据几何关系有: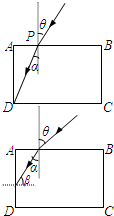
sinα=
=AP AP2+AD2
=d d2+(2d)2 5 5
根据折射定律有:n=sinθ sinα
解得:角θ的最小值为 θ=arcsin5 5
(2)如图,要此光束在AD面上发生全反射,则要求射至AD面上的入射角β应满足:β≥C
则sinβ≥sinC
又 sinC=1 n
根据数字知识有:sinβ=cosα=
=1-sin2α 1-(
)2sinθ n
联立以上三式得:
≥1-(
)2sinθ n 1 n
解得:θ≤arcsinn2-1
所以要此光束直接射到AD面上能在AD面上全反射,角θ的范围为:arcsin
<θ≤arcsin5 5
.n2-1
答:
(1)若要使光束进入长方体后能射至AD面上,角θ的最小值为arcsin
.5 5
(2)若要此光束在AD面上发生全反射,角θ的范围是arcsin
<θ≤arcsin5 5
.n2-1
