问题
选择题
截面为等腰三角形的三棱镜,它的两个底角都为30°,棱镜的折射率为
.两条平行光线垂直于棱镜底面入射,如图所示,两条光线由棱镜射出时所成的角度为( )2
A.30°
B.60°
C.90°
D.120°
答案
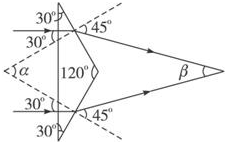
作出光路图.由棱镜材料的临界角:sinC=
=1 n
=1 2
,得C=45°,从题图由几何知识可知,光线从棱镜内射向另一侧面时的入射角i=30°<C,所以光线从侧面折射出去,根据折射定律得2 2
n=
,得sinr=nsini=sinr sini
×sin30°=2
,则r=45°,2 2
同理可知,第二条出射光线的折射角也是45°,
从图中的四边形可求出α=360°-120°-90°-90°=60°,
β=360°-135°-135°-α=90°-60°=30°,所以A正确.
故选A
