问题
填空题
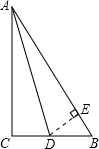
在Rt△ABC中,∠A=30°,∠C=90°,∠A的平分线AD交BC于D,且AD=
|
答案
如图,作DE⊥AB于E点,
∵∠C=90°,∠A的平分线AD交BC于D,
∴DE=CD,
设CD=x,由勾股定理得:AC=AE=
,6-x2
∵∠A=30°,
∴∠B=60°,
∴BE=
x,DB=3 3
x,2 3 3
∴BC=CD+BD=x+
x2 3 3
AB=AE+EB=
+6-x2
x,3 3
∵∠A=30°,∠C=90°,
∴AB=2BC,
即:
+6-x2
x=2(x+3 3
x)2 3 3
解得:x=
x,3- 3 2
∴BC=x+
x=2 3 3
(1 2
+1),3
故答案为:
(1 2
+1).3