问题
计算题
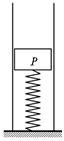
（12分）如图所示，在竖直的光滑套管中有一根劲度系数k= 800N/m、长30cm的轻弹簧。现让质量m=4kg的物块P与弹簧上端轻轻接触并静止释放，则物块P将在套管中做简谐运动。取平衡位置为重力势能零点，弹簧处于原长时弹性势能为零，（g= 10m/s2）。求：
（1）物块P振动加速度的最大值am和振幅A；
（2）弹簧的最大弹力Fm和振动系统的最大势能Epm。
答案
（1）am=10m/s2，A=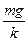
（2）2J
（1）放手时，物块P处在最高点，离开平衡位置的位移最大，加速度也最大。
由于物块P在最高处只受重力
所以物块振动的最大加速度 am=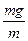
= 10m/s2． （2分）
物块在平衡位置时，有 F=mg， （2分）
由胡克定律得振幅 A=
． （2分）
（2）由简谐运动的对称性可知
物块P在最低点对平衡位置的位移大小与在最高点时的相等（1分）
弹簧被压缩的最大长度为 xm= 2A， （1分）
所以弹簧的最大弹力 Fm=kxm， （1分）
得 Fm= 2mg= 80N． （1分）
物块P在最高处时速度为零，动能最小，由机械能守恒可知势能最大（弹性势能为零，重力势能最大）， （1分）
所以振动系统的最大势能 Epm=mgA=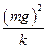
= 2J． （1分）
