问题
问答题
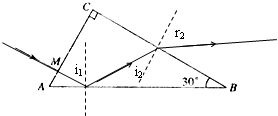
如图所示,截面为直角三角形ABC,∠B=30°,斜边AB=a.棱镜材料的折射率为n=
.在此截面所在的平面内,一条光线在距A点为a/8处的M点垂直AC射入棱镜,不考虑光线沿原路返回的情况,光线从玻璃砖的BC边射出.求:2
(1)光从棱镜第一次射出时的折射角;
(2)光从棱镜第一次射出时的射出点与B点间的距离.

答案
(1)设玻璃砖的临界角为C.则有sinC=
=1 n 1 2
得:C=45°
由几何知识知:光线在AB面上的入射角 i1=60°>C,所以光线在AB上发生全反射.
根据反射定律和几何关系得知光线在BC面上的入射角 i2=30°<C,可知光线将从BC面上射出玻璃砖.
设光从棱镜第一次射出时的折射角为r2.
则有:n=sinr2 sini2
得:sinr2=nsini2=
×sin30°=2
,2 2
r2=45°.
(2)根据几何知识得:AD=
=2AM=AM cos60° a 4
BD=AB-AD=a-
=a 4
a3 4
故EB=
=
BD1 2 cos30°
=
×1 2
a3 4 3 3
a3 4
答:(1)光从棱镜第一次射出时的折射角是45°;
(2)光从棱镜第一次射出时的射出点与B点间的距离是
a.3 4