(选修:3-4)
(1)如图所示为某介质中一列简谐横波的图象,若波的周期为2.0s,a、b、c为介质中三个相同的质点.以下说法正确的是:
A.波的传播速度为4m/s
B.若这一时刻b点的速度方向沿y轴正方向,则波沿x轴负方向传播
C.图示时刻质点a、b、c的加速度大小之比为1:2:3
D.经过l.0s,质点a、b、c通过的路程均为60cm
(2)一半径为R的
球体放置在水平面上,球体由折射率为1 4
的透明材料制成.现有一束位于球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示,已知入射光线与桌面的距离为3
R.求出射角θ.3 2
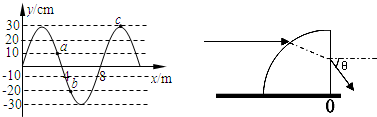
(1)A、由图读出波长为λ=8m,则周期T=
=λ v
s=4s.故A正确.8 2 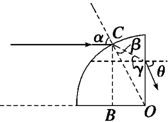
B、若这一时刻b点的速度方向沿y轴正方向,则波沿x轴正方向传播.故B错误.
C、图示时刻质点a、b、c的位移大小之比为:1:2:3,根据简谐运动的特征:a=-
得到加速度大小之比为1:2:3.故C正确.kx m
D、时间t=1.0s=
,质点通过的路程是两个振幅,即为为60cm.故D正确.T 2
故选ACD
(2)设入射光线与
球体的交点为C,连接OC,OC即为入射点的法线.因此,图中的角α为入射角.过C点作球体水平表面的垂线,垂足为B.依题意,∠COB=α.1 4
又由△OBC知sinα=
…①3 2
设光线在C点的折射角为β,由折射定律得n=
=sinα sinβ
…②3
由①②式得β=30°…③
由几何关系知,光线在球体的竖直表面上的入射角γ(见图)为30°.
由折射定律得
=sinγ sinθ
=1 n 3 3
因此sinθ=
,解得:θ=60°.3 2
答:出射角为60°.
