问题
问答题
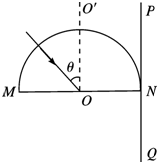
半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一束复色光沿半径方向与OO′成θ=30°角射向O点,已知复色光包含有折射率从n1=
到n2=2
的光束,因而光屏上出现了彩色光带.3
(ⅰ)求彩色光带的宽度;
(ⅱ)当复色光入射角逐渐增大时,光屏上的彩色光带将变成一个光点,求θ角至少为多少?
答案
(ⅰ)由折射定律
n=
,n2=sinβ1 sinα sinβ2 sinα
代入数据,解得:
β1=45°,β2=60°
故彩色光带的宽度为:Rtan45°-Rtan30°=(1-
)R3 3
(ⅱ)当所有光线均发生全反射时,光屏上的光带消失,反射光束将在PN上形成一个光点.即此时折射率为n1的单色光在玻璃表面上恰好先发生全反射,故
sinC=
=1 n1 1 2
即入射角θ=C=45°
答:(ⅰ)彩色光带的宽度为(1-
)R;3 3
(ⅱ)当复色光入射角逐渐增大时,光屏上的彩色光带将变成一个光点,θ角至少为45°.
