问题
计算题
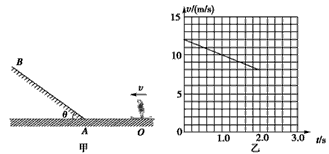
滑板运动是一项陆地上的“冲浪运动”,如图甲所示,OAB是同一竖直平面上的滑行轨道,其中OA段是长27m的水平轨道,AB段是倾角θ=37°足够长的斜直轨道,OA与AB在A点平滑连接。已知滑板及运动员总质量为60kg,运动员从水平轨道向左滑向斜直轨道,滑到O点开始计时,其后一段时间内的运动图象如图乙所示。将滑板及运动员视为质点,滑过拐角时速度大小不变,在水平和斜直轨道上滑板和接触面间的动摩擦因数相同。(取g=10m/s2,sin37°=0.6,cos37°=0.8,忽略空气阻力)求:
(1)滑板与接触面间的动摩擦因数;
(2)运动员到达坡底A点时速度大小;
(3)运动员沿坡上滑的最大距离。(保留三位有效数字)
答案
解:(1)由运动图象知a=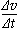 =-2m/s2
=-2m/s2
在水平方向由牛顿第二定律得:-μmg=ma
联立解得:μ=0.2
(2)设人运动到A点时速度为v,由运动学公式v2-v02=2ax
解得:v=6m/s
(3)运动员冲上斜面后做匀减速运动,设减速过程的加速度为a′
由牛顿第二定律得:-mgsinθ-μFN=ma′
FN=mgcosθ
解得:a′=-7.6m/s2
设沿坡上滑的最大距离为x,由运动学公式:0-v2=2a′x
解得:x=2.37m
即沿坡上滑的最大距离为2.37m
