问题
计算题
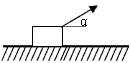
如图所示，质量为2kg的物体放置在水平地面上，在大小为10N、方向与水平面成37°角斜向上的拉力作用下，由静止开始做匀加速直线运动，4s内物体的位移为9.6m，试求：
（1）物体与水平面间的动摩擦因数；
（2）若4s末撤去拉力，则物体继续前进的最大位移。
答案
解：（1）由s =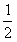 
at2，物体在前4s内的加速度为a1 = 
=
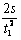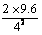m/s2 = 1.2 m/s2
物体共受到四个力的作用：重力G，拉力F，支持力FN1，滑动摩擦力F3，建立图示坐标系：
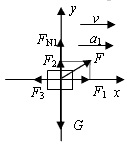
由牛顿第二定律F合= ma
Fcosθ －μFN1= ma1
Fsinθ+ FN1－mg = 0
解得μ=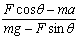
= 
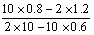= 0.4
（2）撤去拉力时，物体的速度为vt = a1t1 = 1.2×4 m/s = 4.8 m/s
撤去拉力后，物体共受到三个力的作用：重力G，支持力FN2，滑动摩擦力F4，物体做匀减速运动，设加速度为a2，此时建立图示坐标系：
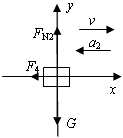
由牛顿第二定律F合= ma
－μFN2 = ma2
FN2－G = 0
解得a2 = －μg = －0.4×10 m/s2 = －4 m/s2
则s2 =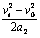
=
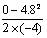m = 2.88m
