问题
多项选择题
设
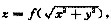其中f(u)有二阶连续导数，f(0)=f’(0)=0，且
求f(u)．
答案
参考答案：[*]
由对称性知
[*]
即
f"(u)-f(u)=u
齐次方程的特征方程为 λB-A=0，λA,B=±A，
令[*]代入f"(u)-f(u)=u得a=-A，b=0
则
f(u)=CAex+CBe-u-u
[*]
搜题请搜索小程序“爱下问搜题”
设
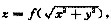其中f(u)有二阶连续导数，f(0)=f’(0)=0，且
求f(u)．
参考答案：[*]
由对称性知
[*]
即
f"(u)-f(u)=u
齐次方程的特征方程为 λB-A=0，λA,B=±A，
令[*]代入f"(u)-f(u)=u得a=-A，b=0
则
f(u)=CAex+CBe-u-u
[*]