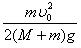问题
计算题
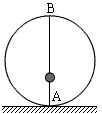
如图所示，圆环的质量为M，经过环心的竖直细钢丝AB上套一质量为m的小球，今将小球沿钢丝AB以初速度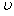
0从A点竖直向上抛出，致使环对地面的压力恰好为零，求：
（1）小球上升的加速度；
（2）小球能达到的最大高度。（球不会碰到B点）
答案
解：（1）环对地面的压力恰好为零，说明它所受小球的滑动摩擦力F1与环自身重力G1恰平衡，所以二者大小相等，即：F1=G1=Mg
小球受力如图，其中F2与F1为作用力和反作用力关系，大小相等，所以F2=Mg
由牛顿第二定律得：F2+G2=ma
所以小球上升的加速度大小为：a=(F2+G2)/m=(M+m)g/m
小球上升的加速度方向竖直向下
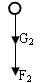
（2）小球上升到最高点时速度等于零，由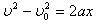
得：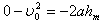
所以小球能上升的最大高度hm=