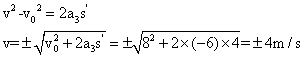问题
计算题
如图所示,在水平地面上固定一倾角为37°足够长的的斜面,今有一木块以初速度8m/s冲上斜面,木块与斜面的动摩擦因数为0.25,(最大静摩擦力近似等于滑动摩擦力,sin37°=0.6,cos37°=0.8,g=10m/s2)则:
(1)木块沿斜面上升的最大距离为多少?
(2)木块在斜面上运动的时间为多少?
(3)如果斜面是光滑的,求木块运动到离斜面底端4m处的速度?

答案
解:(1)对木块分析受力如图
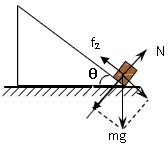
根据牛顿第二定律有mgsinθ+f1=ma1
f1=μN
N=mgcosθ
联立以上可得加速度为a1=g(sinθ+μcosθ)=8m/s2
物体沿斜面做匀减速运动,根据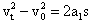
可得木块沿斜面上升的最大距离为
(2)木块上升到最高点所用的时间t1,
木块上升到最高点后的受力如图(“略”)

故木块不能停留在斜面上,将沿斜面下滑,
下滑的加速度为a2=4m/s2
木块下滑的时间为t2
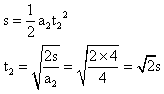
木块在斜面上运动的总时间为t=t1+t2=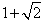 s
s
(3)如果斜面是光滑的,木块上升到最高点后将沿斜面返回,在斜面上的加速度不变,加速度大小为a3=gsin37°=6m/s2
木块离斜面底端4米时的速度