问题
计算题
质量为M,倾角为θ的直角劈静置于光滑水平地面上。质量为m的物体放在劈的斜面上,如图所示,设M=2.0kg,m=1.0kg,θ=37°。物体与劈面间的动摩擦因数μ=0.25。
(1)若直角劈M静止不动,求物体运动的加速度大小;
(2)现对劈施以水平向左的推力F,要使物体与直角劈斜面相对静止,则推力F应满足什么条件?(设物体与斜面间的最大静摩擦力等于滑动摩擦力,sin37°=0.6,cos37°=0.8)
答案
解:(1)对物体m受力分析如图所示
沿斜面方向由牛顿第二定律:mgsin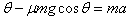
a=g(sinθ- =
=
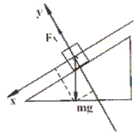
(2)由题意知,当F取最小值时m恰好不下滑,对物体m受力分析如图所示

y方向上由平衡条件: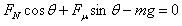 ①
①
X方向由牛顿第二定律得: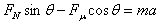 ②
②
又F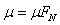 ③
③
联立①②③式解得a=5m/s2
对整体分析由牛顿第二定律得: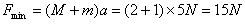
由题意知,当F取最大值时m恰好不上滑,对物体m受力分析如图所示(“略”)
Y方向上由平衡条件得 ④
④
X方向由牛顿第二定律得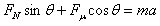 ⑤
⑤
联立③④⑤式解得a=12.3m/s2
对整体分析由牛顿第二定律得: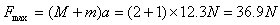
综上得要使m相对M不滑动F必须满足的条件是15N≤F≤36.9N
