如图所示,长L=6m的水平传输装置,在载物台左端物块以初速度v0=3m/s滑入传送带。物块与传送带之间的动摩擦因数μ=0.5,g=10m/s2,求:
(1)当传送带静止时,物块在传送带上运动的加速度a大小;
(2)当传送带静止时,物块滑上传送带向右运动的最远距离s;
(3)当传送带以恒定的速率v=6m/s沿顺时针方向匀速转动时,物块从滑上传送带到离开传送带所经历的时间t。

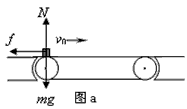
解:(1)当传送带静止时,物块受力分析如图a所示,则由牛顿第二定律可得:

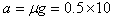 m/s2=5 m/s2
m/s2=5 m/s2
(2)由匀变速直线运动公式: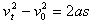
可得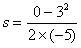 m=0.9m<L
m=0.9m<L
所以当传送带静止时,物体滑上传送带向右运动的最远距离为0.9m
(3)当传送带以恒定的速率v=6m/s沿顺时针方向匀速转动时,物块速度比传送带速度小,故受到摩擦力向右,如图b所示
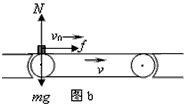
则物块的加速度为: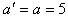 m/s2
m/s2
设物块达到传送带速度的时间为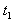 :
: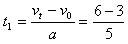 s=0.6s
s=0.6s
这段时间物块通过的位移为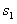 :
: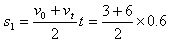 m=2.7m<L
m=2.7m<L
故物块先匀加速后与传送带共速,最后从右边离开传送带,设共速后运动的时间为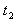 ,可得:
,可得:
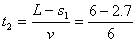 s=0.55s
s=0.55s
综上述,物体从滑上传送带到离开传送带所经历的时间t: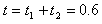 s+0.55s=1.15s
s+0.55s=1.15s

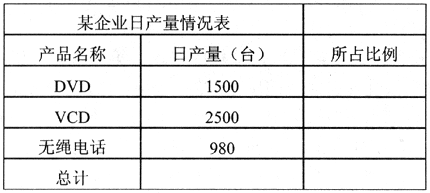 (2)选取“日产量情况表”中“产品名称”和“所占比例”列(不包括“总计”行)的单元格的内容建立“簇状柱形图”,x轴上的项为产品名称(系列产生在“列”),标题为“日产量情况图”,插入到表的A8:E19单元格区域内。
(2)选取“日产量情况表”中“产品名称”和“所占比例”列(不包括“总计”行)的单元格的内容建立“簇状柱形图”,x轴上的项为产品名称(系列产生在“列”),标题为“日产量情况图”,插入到表的A8:E19单元格区域内。