问题
计算题
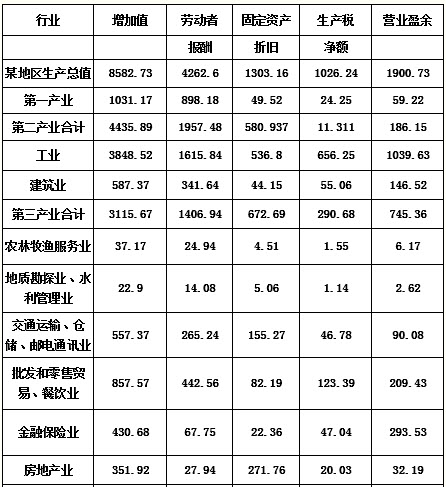
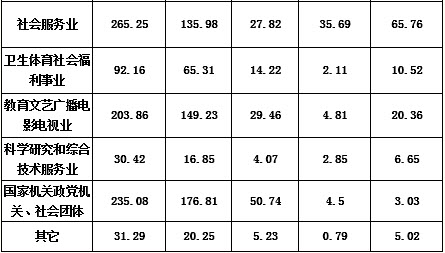
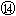如图所示，一质量为m=1kg的小滑块从半径为R＝0.8m的光滑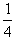
圆弧轨道顶端静止释放。到达圆弧轨道底端时恰好滑上上表面与圆弧轨道底端相切的木板，木板的质量M=1kg。开始静置在水平地面上，小滑块滑上木板后，木板开始向右滑动，最终小滑块以vm=2m/s的水平速度飞离木板。己知木板高h＝0.8m，小滑块与木板间的动摩擦因数为μ1＝0.4，木板与水平地面间的动摩擦因数为μ2＝0.1，g取10m/s2。求：
（1）小滑块滑至圆弧轨道最底端时，圆弧轨道对小滑块的弹力大小；
（2）小滑块飞离木板时木板的速度大小；
（3）小滑块从滑上木板到落至水平地面的过程中，小滑块在水平方向上移动的距离。
答案
解：（1）小滑块在圆弧轨道运动过程中，由机械能守恒可知：
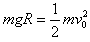①
得：v0＝4m/s ②
当小滑块滑至圆弧轨道底端瞬间，由牛顿第二定律可知：
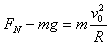③
得：FN＝30N ④
（2）小滑块滑上木板后，由牛顿第二定律可知：
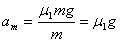＝4m/s2 ⑤
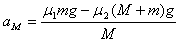＝2m/s2 ⑥
又：vm＝v0－amt ⑦
vM＝aMt ⑧
由⑤⑥⑦⑧得：t＝0.5s ⑨，vM＝1m/s ⑩
（3）小滑块水平飞离木板后：
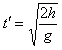＝0.4s 
又：sm＝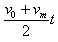
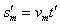
小滑块从滑上木板到落地的过程中，小滑块在水平方向移动的距离
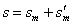＝2.3m 
