问题
计算题
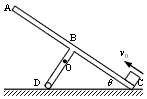
如图所示,ABCD是一个T型支架,AC与BD垂直,且AB=BC。已知整个支架的质量为M=9kg,重心在BD上离D点为l=0.4m的O点处,BD长为d=0.6m,支架可绕位于水平地面上且过D点的水平轴无摩擦地转动,AC为一斜面,与水平地面间的夹角为θ=37°,C处搁在地面上,现有两个质量均为m=2kg的小滑块由位于C处的弹射器(图中未画出)以v0=6m/s的初速度沿斜面相继弹出而滑上AC斜面,两个滑块弹出的时间差为△t=0.1s,小滑块与斜面间的动摩擦因数为μ=0.5。求:
(1)小滑块沿斜面向上滑的加速度大小;
(2)第二个滑块弹出多少时间时支架将翻转。
答案
解:(1)mgsinθ+μmgcosθ=ma
a=gsinθ+μgcosθ=(10×0.6+0.5×10×0.8)m/s2=10m/s2
(2)设第二个滑块滑上的距离为s,对支架由力矩平衡条件得:
Mglsinθ=2μmgdcosθ+mgcosθ(s1-L/2)+mgcosθ(s2-L/2)
s2=v0t-at2/2
s1=v0(t+△t)-a(t+△t)2/2 10×10×0.4×0.6=2×0.5×2×10×0.6×0.8+2×10×0.8(6t-5t2-0.8)+2×10×0.8[6t+0.6-5(t+0.1)2-0.8]
解得:t1=0.2s,t2=1s(不合)
且t1m=v0/a=0.6s,t1<t1m,解答合理
