问题
计算题
如图所示，在倾角为θ的足够长的斜面上，有一质量为m的物体，以初速度v0沿斜面向上运动，已知物体与斜面间的动摩擦因数为μ（μ＜tanθ）。
（1）求物体上滑过程中的加速度大小；
（2）求物体上滑的最大距离；
（3）试应用牛顿第二定律和运动学公式证明：物体下滑过程中损失的机械能等于物体克服摩擦力所做的功。
答案
解：（1）上滑过程由牛顿第二定律得mgsinθ＋μmgcosθ＝ma
得：加速度a＝gsinθ＋μgcosθ
（2）由2ax＝v02－0
得xm＝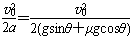
（3）下滑过程中：由牛顿第二定律得mgsinθ－μmgcosθ＝ma′
得：加速度a′＝gsinθ－μgcosθ
由运动学方程2a′xm＝vt2－0
得：vt＝
物体克服摩擦力所做的功为W克f＝fxm＝μmgcosθ·xm
设地面处重力势能为零，则下滑过程损失的机械能为
－ΔE机＝(mgxmsinθ＋0)－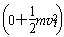
＝mgxmsinθ－m(gsinθ－μgcosθ)xm＝μmgcosθ·xm
所以W克f＝－ΔE机得证
（说明：若学生将xm代入方程证明也正确，表达式为：W克f＝－ΔE机＝μmgcosθ
）