已知函数f(x)=ln(1+x)-p
(1)若函数f(x)在定义域内为减函数,求实数p的取值范围; (2)如果数列{an}满足a1=3,an+1=[1+
|
(1)函数f(x)=ln(1+x)-p
的定义域为[0,+∞),x
f′(x)=
-1 1+x
=p 2 x
.2
-p(1+x)x 2(1+x) x
依题意,2
-p(1+x)≤0恒成立,所以p≥(x
)max,2 x 1+x
由x≥0⇒1+x≥2
⇒x
≤1,知(2 x 1+x
)max=1,2 x 1+x
∴p≥1,∴p的取值范围为[1,+∞).
(2)首先,由a1=3,得a2=[1+
]×3+1 12×22
=4,1 4
而当an>0时有an+1-an=
an+1 n2(n+1)2
>0,∴an+1>an,1 4n
所以,对n∈N*(n≥2),都有an≥4.
再由an+1=[1+
]an+1 n2(n+1)2
及an≥4,1 4n
又得an+1≤[1+
]an+1 n2(n+1)2
=[1+an 4n+1
+1 n2(n+1)2
]an,1 4n+1
∴lnan+1≤ln{[1+
+1 n2(n+1)2
]an}=ln[1+1 4n+1
+1 n2(n+1)2
]+lnan,1 4n+1
∴lnan+1-lnan≤ln[1+
+1 n2(n+1)2
].1 4n+1
由(1)知当p≥1时f(x)为减函数,取p=1,则f(x)=ln(1+x)-
,x
当x>0时f(x)<f(0)=0,故ln(1+x)≤
(x>0),x
∴lnan+1-lnan≤ln[1+
+1 n2(n+1)2
]<1 4n+1
<
+1 n2(n+1)2 1 4n+1
+1 n(n+1)
=1 2n+1
-1 n
+1 n+1
,1 2n+1
∴lna3-lna2<
-1 2
+1 3
,lna4-lna3<1 23
-1 3
+1 4
,….,lnan-lnan-1<1 24
-1 n-1
+1 n
,1 2n
将这n-2个式子相加得lnan-lna2<
-1 2
+1 n
(1-1 4
)<1 2n-2
,3 4
∴
<ean a2
,将a2=4代入得an<4e3 4
,3 4
故当n≥2时,4≤an<4e
.3 4

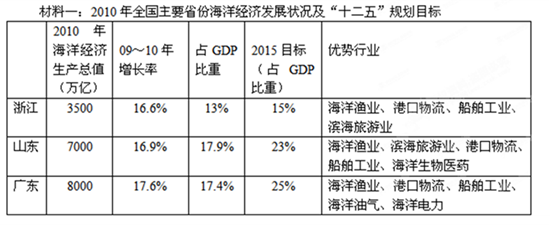
 港口物流、船舶工业是传统产业,海水综合利用、海洋新能源、海洋生物医药、深海资源勘探开发等新兴海洋产业在我国目前还处于边缘状态。我国海洋产业内部结构也存在粗放型产品多、高附加值产品少现象。海洋科技对海洋经济的贡献率只有30%左右,而一些发达国家已达70%-80%。
港口物流、船舶工业是传统产业,海水综合利用、海洋新能源、海洋生物医药、深海资源勘探开发等新兴海洋产业在我国目前还处于边缘状态。我国海洋产业内部结构也存在粗放型产品多、高附加值产品少现象。海洋科技对海洋经济的贡献率只有30%左右,而一些发达国家已达70%-80%。 、宽领域、深层次的开发,就一定能使大海成为浙江经济 “扬帆远航” 的“蓝色引擎”。
、宽领域、深层次的开发,就一定能使大海成为浙江经济 “扬帆远航” 的“蓝色引擎”。 、中企业成长起来的,没有天生的大企业;其次,大企业起龙头骨干作用,其他中小企业跟随、不可缺少,相互不可替代;再次,一些发达的国家,它们在小企业的问题上仍然也有着很值得学习的地方,大企业可以“大而强”,小企业也可以“小而强”、“小而精”,我们自己也有这样的一些小的企业搞的很好,这值得我们思考。
、中企业成长起来的,没有天生的大企业;其次,大企业起龙头骨干作用,其他中小企业跟随、不可缺少,相互不可替代;再次,一些发达的国家,它们在小企业的问题上仍然也有着很值得学习的地方,大企业可以“大而强”,小企业也可以“小而强”、“小而精”,我们自己也有这样的一些小的企业搞的很好,这值得我们思考。 表描述浙江海洋经济发展总体状况。
表描述浙江海洋经济发展总体状况。