问题
计算题
一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ。初始时,传送带与煤块都是静止的,现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动求此黑色痕迹的长度。
答案
解法一:根据“传送带上留下了一段黑色痕迹” 可知,煤块与传送带之间发生了相对滑动,煤块的加速度a小于传送带的加速度a0。根据牛顿第二定律可得a=μg
设经历时间t,传送带由静止开始加速到速度等于v0,煤块则由静止加速到v,有v0=a0t,v=at
由于a<a0,故v<v0,煤块继续受到滑动摩擦力的作用
再经过时间t',煤块的速度由v增加到v0,有v0=v+at'
此后,煤块与传送带运动速度相同,相对于传送带不再滑动,不再产生新的痕迹
设在煤块的速度从0增加到v0的整个过程中,传送带和煤块移动的距离分别为x0和x,有

传送带上留下的黑色痕迹的长度l=x0-x
由以上各式得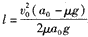
解法二:利用相对运动求解设皮带加速时间为t1
v0=a0t1
此时煤块速度(相对于传送带)v=(a0-μg)t1
相对位移为

